Getting To Mars

Edit: updated to include Aldrin Cyclers

There are multiple ways to get to Mars, and each has pros and cons. The one thing they all have in common is orbital mechanics. Some options can get to Mars in a short period of time, while others could take up to a year. Some are better suited for robotic missions, others for crewed missions. This article takes a look at the problems of getting to Mars (and getting back) and what options are available.

There are some terms that you may be familiar with, but are generally not well understood or misunderstood. Let's begin with these before moving on.

On Mars, the day is almost 40 minutes longer. Since it is both awkward and confusing to have a clock run on an extra 39 minutes and 35 seconds before resetting, Mars was given its own clock which resets after 24 hours in the same way clocks do here on Earth. To achieve this, the Martian second is stretched a little. A Martian second is approximately 1.02749 universal seconds. This gives the Martian clock the same number of seconds per day as on Earth (86,400 in case you were interested).

Incidentally, when early missions to Mars reached their destinations, the mission teams were issued watches that kept Martian time. They were nothing special, just off-the-shelf-watches adjusted to run a bit slower.

A Martian day is referred to as a sol to differentiate it from an Earth day. This is important, because dates in the Martian Calendar do not keep step with dates on Earth. For example, if you look for the dates Feb 9^th 2020 and Jan 3^rd 2020 on the Mars Weather page, you'll notice they're missing, yet the sol numbers for the days to each side of them are continuous. This is because there is an extra day here on Earth for every 36 sols (a sol is approximately 1/36^th of a day longer).

To avoid confusion, from this point on, whenever you see 'day' in this article, it refers to an Earth day, and 'sol' describes the Martian equivalent.

The synodic period is the amount of time that it takes for a celestial object to reappear at the same point in relation to two or more other celestial objects. The synodic period for Mars uses Earth and the sun as the other two objects. The synodic period of Mars is longer than its year (686.971 days) because of of the movement of the Earth, and amounts to 779.96 days.

The synodic year is important, because it defines the regularity with which launch periods occur for journeys that use Hohmann transfer orbits.

Isaac Newton and Johannes Kepler before him, thought of gravity as a force that pulled on objects such as planets and moons. Einstein though, determined that gravity distorts space. The Moon orbits the Earth because it is travelling in a straight line through curved space.

This means that flying 'in a straight line' (as we perceive it) to Mars is simply not possible. Instead, it is necessary to move in some kind of orbit. Most orbits are closed, which means they arrive back at their starting point. There are two types of unclosed orbit: parabolic and hyperbolic. Parabolic orbits have just enough energy to match escape velocity and therefore will never return. Hyperbolic orbits have more than enough energy to achieve escape velocity (and therefore are moving faster), and like parabolic orbits, will never return.

Travelling to Mars from Earth will, at the very least, take several weeks. This makes it necessary for the spacecraft to aim not for Mars, but to where Mars will be in several weeks (or months) time. It's a rendezvous, so it is necessary to plot an orbit that will get the spacecraft to the right place at the right time - and that often requires launching at the correct time.

A launch can occur both from the ground and from orbit (when switching from one orbit to another), so launch periods and launch windows can both refer to a surface launch or launch from orbit.

A launch period is the period when launches are possible. We might say, for example, that the launch period is from 1^st March to 31^st March.

A launch window occurs within a launch period, and there might be (and usually are) multiple windows within a period. In the example above using March as the launch period, we can launch from the surface straight into a Hohmann transfer orbit only once per day, and the window might only be a few seconds long.

Generally speaking, a launch from surface to LEO is preferred, because the window for this is always open. Once in orbit, a window opens to head out to Mars once on each orbit, with an orbit usually taking around 90 minutes (thereby providing many more launch windows per day).

It can be confusing talking about the amount of fuel or energy required to propel a spacecraft to a certain speed, because the mass of one spacecraft differs from another, and the amount of fuel required to achieve the velocity needed also differs with each spacecraft. Some engines are more powerful than others too, and the spacecraft might have more than one engine. This leads to different lengths of time the engines might be run.

What doesn't change are the velocities. Rather than talk about fuel or energy, it becomes easier to talk about the velocity in terms of going from one velocity to another. Then, for each specific mission, someone can work out the amount of fuel required and the length of engine runtime.

Delta-v - usually indicated using the symbols ΔV - literally means “change in velocity”, so if the delta-v is 2.6 km/s, then the spacecraft must gain 2.6 km per second in speed. The lower the delta-v, the less fuel (often referred to as propellent) is required and this is often accompanied by shorter engine runtime.

Delta-v can be negative, indicating the spacecraft must decelerate, but in orbital terms this is usually accomplished by a retrograde acceleration (engines facing the direction of travel, effectively slowing the spacecraft down) and to keep things simple, ΔV is usually just expressed as a positive value, since ultimately it refers to fuel consumption. Orbital mechanics can be a little mind-mushing like that, but as Albert Einstein once said, everything is relative.

Note: I've used the term runtime rather than burn, because some engines (e.g. plasma and ion engines) don't, strictly speaking, burn their fuel.

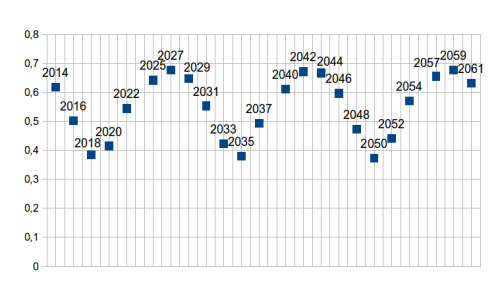For a given method of transfer (e.g. a Hohmann transfer orbit), the amount of ΔV will differ from one transfer period to the next. Earth and Mars are not in a 2:1 ratio orbit synchronicity. A Martian year is approx 687 days, slightly less than 2 Earth years. In addition, the Martian orbit is inclined to the ecliptic. What this means is that on some years, the closest approach of the two planets to each other is closer than on other years.

The chart shows this fluctuation from 2014 through 2061, with the values representing distances in astronomical units (1 AU is the average distance of Earth from the Sun). As you can see, this works on a 15 year cycle. The closer together the two planets get, the lower the ΔV for any given method of transfer.

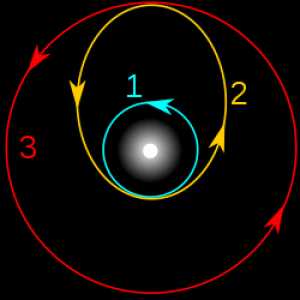This is probably the one most people have heard of. It's properly called the Hohmann Transfer Orbit or Hohmann Transfer Ellipse. The purpose of this is to go from a low orbit to a higher one or vice versa. If you have a satellite that needs to go into the very high geostationary orbit (approx 35,000km above sea level), it is easiest to put it into a low Earth orbit, then use a Hohmann transfer orbit to get to where it needs to be.

When the journey is from Earth to Mars, you have to consider that both Earth and Mars are in orbit around the Sun. Earth's orbit represents a low solar orbit, and Mars' orbit the high solar orbit. The manoeuvre is the same as the one taking the satellite to a geostationary orbit, but the Sun becomes the host gravitational mass and everything is on a much grander scale.

Imagine your starting point is an orbit around the Earth. The Hohmann transfer orbit describes an ellipse where one end is at the Earth and the other is at Mars, and for the sake of simplicity, let's make the planets themselves stationary. To begin with, it is necessary to leave Earth orbit and get on the Hohmann transfer orbit. To do so it is necessary to expend a large amount of energy to speed the spacecraft up.

This is where we come to ΔV (see Delta-V above). To get onto a Hohmann transfer orbit from Earth, you need to increase speed by an average of 2.9km/s. Average? It turns out that on some years the ΔV is less than on others, and this variance follows a 15 year cycle (this is also explained in Delta-V above).

Note: For the rest of this discussion, we'll assume an 'average' year. On other years, the duration of the journey and the exact ΔV will vary.

The journey to Mars will take around 258 days (8.5 months or so). When the spacecraft gets there, it must speed up to the same speed that Mars is travelling around the Sun. That will require a ΔV of 2.6km/s. After that, there will probably be a Mars Orbital Injection burn to go into orbit around Mars, requiring around 3.3km/s ΔV. In some instances this may not be necessary (see Ballistic Capture below).

That's how it works when planets are stationary, which unfortunately they aren't. It is necessary to launch from Earth at a time such that Mars will be at the apex (aphelion) of the Hohmann transfer ellipse 258 days later. In other words, both planets must be in the correct position in their orbits when the mission launches or the spacecraft will miss Mars. This is where the synodic period comes in, and for Earth/Mars that means the planets are only in the right positions once every 26 months.

One of the benefits of the Hohmann transfer is that it requires (relatively) low amounts of energy. The total ΔV is around 4.5 km/s. Once the spacecraft has transferred onto the Hohmann ellipse, the spacecraft shuts down its engines and cruises until it has to get off the ellipse at Mars. Because of this, it is sometimes referred to as a low-energy transfer.

Another problem with Hohmann transfers is the time. For a planned resupply mission, or for sending a satellite or lander to Mars, that's not a problem, but humans don't like absorbing the radiation doses they'll get in space as they depart Earth's protective magnetic field. This means either modifying the spacecraft to protect them better (adding even more mass to an already large-mass craft), repurposing mass that is already on board (such as water) to use as a radiation shield, or send the crew there on a faster route.

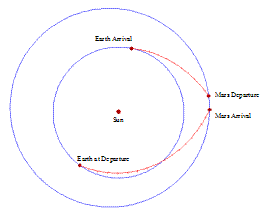This is also sometimes called a fast transfer, because it really is. A Hohmann transfer takes nearly 9 months to get to Mars, whilst on-orbit staging can do it in 120 days (4 months). Further, it can achieve a round-trip (Earth-Mars-Earth) of 209 days, including a 14 day stay at Mars. A longer stay is possible with a total mission time of 245 days. It achieves this through the use of hyperbolic or parabolic orbits which would take the spacecraft right past Mars and into the outer solar system. As it approaches Mars, it expends large amounts of fuel to decelerate enough to be captured into a Martian orbit.

On-orbit staging works by lifting the spacecraft into low Earth orbit (LEO) in sections, which are then assembled in orbit. The fuel for the return journey is already located in orbit around Mars. Not having to take this fuel - which isn't needed for the outward journey - decreases the total mass of the vessel and therefore decreases the fuel requirement. Fuel usually accounts for around 90% of the mass of a non-satellite spacecraft.

The total ΔV required for this kind of journey is enormous, in the region of 30-40km/s. The hyperbolic trajectory the spacecraft is on is an escape trajectory that will take the spacecraft out of the solar system, and the spacecraft is travelling at tremendous speed. It is necessary to shed that speed on arrival at Mars or the spacecraft will shoot off into the outer solar system heading for interstellar space, and will likely never be seen again. The spacecraft will be going too fast to use aerobraking in the Martian atmosphere to slow down, so expenditure of fuel is the only option.

Likewise, the return journey is just as fast, and velocity must be shed or the spacecraft will head out into the outer solar system.

Like Hohmann transfers, there is a period when these transfers can take place. It is, however, slightly more flexible.

Ballistic capture is an interesting development that evolved out of the Moon missions in the 1960's. The idea was to get into the Moon's orbit around the Earth, but ahead of where the Moon actually was. If the spacecraft is orbiting slightly slower than the Moon, the Moon will catch up until its own gravity draws the spacecraft into orbit about itself.

There are two main advantages to this technique. The Lunar orbit capture is achieved for free - there is no expenditure of fuel. This means the spacecraft can leave Earth with less mass (making it a cheaper endeavour) or with more mass in the payload section for the same price. The Japanese proved the viability of this technique in the Hiten mission in 1991.

The big problem was that for a long time it was believed it couldn't be used in a Mars mission. The gravitational effects of the Earth, Moon, Mars, the Sun and Jupiter all had to be taken into consideration. They think they've cracked the maths now, and perhaps we'll see missions in the 2020's that'll prove the concept.

Because there is no insertion burn at Mars, this is an LET (low-energy transfer). It does take up to one year to complete the transfer, but take careful note of the words 'up to'; it can take less, right down to only slightly more than a Hohmann transfer. The enormous advantage of ballistic capture is there are no specific launch periods - launches can occur at any time. This means that supplying a crewed surface mission can take place regularly and indefinitely, so long as funds are available and there is a will to keep doing so. The actual journey from Earth to Mars orbit is achieved through a Hohmann transfer ellipse. The cost of the ΔV to get off the transfer orbit still has to be paid, but at a slightly lower price because the spacecraft isn't trying to orbit the Sun as fast as Mars and there is no Mars Orbital Injection to get into orbit around the planet.

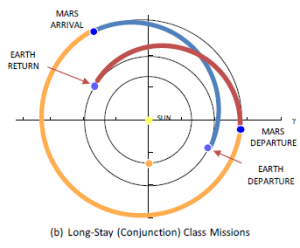
NASA and other space agencies have been looking at other ways to construct a mission profile. One of the interesting ones comes from NASA and is described in their DRA 5.1 and later documents. In the diagram to the left, a long-stay mission profile is described. The stay time varies from 400 to 900 days, and the total round-trip time varies from 800 to 1100 days depending on the mission profile and during which part of the 15 year cycle the mission takes place.

Long-stay missions bring several benefits: the crew get time to adjust to gravity again before beginning the science mission in earnest, and the ΔV is minimal. They would though, have plenty of time to conduct a wide variety of science missions, and not be forced to hurry through their schedule - although you can be sure they'll be kept busy. The downside is the crew need provisions to last them the duration, which is going to be measured in years. This would also require the transport vessel to be larger and have more mass, which increases the fuel requirement to achieve the ΔV. At a technological level, the life-support equipment must be constructed to last the duration. All of this massively increases the costs of a mission. Sending provisions and life-support ahead of the crew mitigates the 'very big ship' and enormous ΔV scenarios.

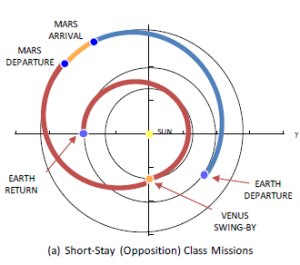Shorter stay-times means the life-support equipment is cheaper. Habitats, for example, need only last a few weeks rather than years. This article isn't really about mission profiles, but you can bet your bottom dollar that someone has looked at short-stay missions just so they can examine them for their upsides and downsides. The long-stay routes seen above look very similar to Hohmann transfer orbits, and for good reason - they are.

What about short-stay missions then? Well, it turns out that the piper still needs to be paid. If you have a short stay, you'll have a very long transfer period. Looking at the image to the right, you'll see the outward journey is the same as for the long-stay mission: it's a Hohmann transfer orbit. On the return journey though, you can see a flyby of Venus and a loop around the sun, greatly extending the flight time. As it happens, getting creative like this and using Venus for a flyby can work in both the outward and the return journeys. The big problem on the return journey is shaving off speed - the spacecraft is falling down the sun's gravity well.

The Venus flyby and loop around the sun help with this - once past Venus, the spacecraft is heading for an Earth rendezvous and is climbing up the sun's gravity well, shedding speed.

Short-stay missions might total 20 months, but don't get the wrong impression from the image: these missions can be configured in different ways and by accepting a complete loop around the sun (and perhaps a bit more), the duration of the stay becomes more flexible. Many of the technical issues of a long-stay mission evaporate, but the crew may spend a large amount of time in space, and that means they need to carry more provisions with them, so the vessel gets large and the fuel requirements increase.

Every minute an astronaut/cosmonaut/taikonaut spends in space is a hazard, especially when they are outside the Earth's very protective magnetosphere. Not only are they subject to harmful radiation, but their equipment is too. It should be remembered that cosmic radiation can damage silicon chips. It should also not be forgotten that they are not the only things in interplanetary space. The trade-off between cost and time is also reflected in crew safety: the cheaper the mission, the less safe the crew are. This leaves the space agencies with a dilemma. They must fulfil the mission at the cheapest possible price while keeping the crew safe and still having a reasonable chance of the mission being a success. The higher the cost of a mission, the bigger the onus on the agency to have a successful mission. Getting to Mars (with or without a crew) is a very expensive business.

A Mars cycler is an elliptical orbit (green) that crosses the orbits of Earth (blue) and Mars (red), and encounters both planets at the points where it crosses their orbits, although not necessarily on every orbit.

Cycler orbits are those that regularly visit two or more celestial bodies. Over a hundred ballistic Earth-Mars cyclers have been discovered, and hundreds more non-ballistic cyclers. Non-ballistic cyclers require some powered maneuvers. Ballistic cyclers are the most interesting ones - they can get a vessel from one planet to another at no fuel cost.

In 1985, Buzz Aldrin - he of 2nd man on the Moon fame - calculated a cyler orbit which became known as the Aldrin Cycler. This is just one type of Mars cycler, but it's powered by an impressive vision that harks back to the science-fiction of the 1950's. Aldrin describes two types of vessel - taxis and castles.

Taxis take the crew from the planet to the castle and vice versa. This is the only part of the journey requiring the expenditure of fuel. The castles permanently follow the cycler orbit, and provide both a habit of sufficient size it is comfortable for the crew, and a safe haven against the ravages of the interplanetary medium, particularly in regard to radiation.

The really important point of the Aldrin Cycler is the amount of time it takes to travel between the two planets - 146 days. That's less than five months. What's more, you can have several castles in operation at once, granting you the ability to travel to and from Mars at regular intervals, although only the Aldrin Cyclers grant the 146-day transfer period.

Wikipedia has a page on Mars Cyclers that details some of the other cyclers available.

Plasma rocket engines sound very futuristic, but they actually exist and have done for a while. BepiColombo, a spacecraft destined for Mercury and launched in October 2018, uses an ion-plasma engine, a type of solar-electric propulsion system. Ad Astra have been working on their VASIMR plasma engine for some time. Plasma is the fourth state of matter, after solid, liquid and gas. Their engine can heat the propellant (they use argon) somewhere between 5,000,000 and 10,000,000°K.

This movie (from Ad Astra) shows another method of getting to Mars, by swinging out beyond its orbit and then falling back towards Mars again. It is possible because of the capabilities of the VASIMR engine. Note that OTV means orbital transfer vehicle, and means the vehicle that goes from Earth to Mars and vice versa (you could call it the mother ship).

The lander (and crew) depart the OTV as it does a flyby of Mars. The trip to Mars takes just 60 days! The lander has much less mass and can use a powerful chemical reaction rocket to decelerate, as well as having the possibility to use aerobraking to get into orbit prior to making a descent. The OTV continues on for a second rendezvous with Mars 200 days later. After a lengthy surface mission (718 days) the OTV returns to Earth in just 69 days.

The future of crewed missions to other planets just screams out for plasma engines. Nothing else really makes sense, once you have all the benefits of plasma at your fingertips. However, a NEP-VASIMR (Nuclear-Electric Powered Variable Specific Impulse Magnetoplasma Rocket) is a long way off. Nuclear power is required to generate the 200 megawatts required (which, incidentally, is six times more than is generated in a nuclear powered submarine). In space, one of the big problems is dumping heat. It might sound odd, since space is meant to be so cold, but it's building in the efficient radiators large enough to dispel the heat (which adds mass to the vessel) that causes problems.

This has lead to NEP-VASIMR being dubbed a hoax, and certainly the 39 day voyage to Mars is unreachable without it, which just leaves solar-electric VASIMR and conventional chemical reaction rockets for now.

Where we might see VASIMR engines being used, is the delivery of very large payloads to Mars. Don't think bigger rovers than we currently have, think of a fleet of them, all being delivered at once. Although that's an unlikely scenario, delivering all the surface equipment and provisions ahead of a crewed mission might be cheaper if they're sent together. Such a vessel could make the trip several times, reducing costs. As far as plasma engines are concerned, it's really a case of 'watch this space'.

Reducing the cost without endangering either the crew or the mission is difficult. However, fuel is very expensive. Usually, manufacturing the fuel isn't too bad - it's getting it into space. Fuel is very heavy. One way to save on fuel is to head out to Mars from the Moon. Getting to the Moon is not easy, but it is much easier than going to Mars. Once you are there, all sorts of advantages kick in.

Going anywhere requires velocity. The Earth is moving around the sun, so any spacecraft, even if it is still on the launchpad on the surface of the Earth, is already travelling at that speed. If the spacecraft is in orbit around the Earth, it is already travelling even faster. The Moon is in orbit around the Earth, so if you are in orbit around the Moon, you also gain the Moon's velocity plus the orbital velocity (around the Moon). In addition, the Moon's gravity is much lower, so the escape velocity is less (and hence the ΔV is lower). As the spacecraft departs the Moon, the Moon draws away as it continues swinging around the Earth, so the gravitational pull of the Moon drops off even more rapidly.

In addition, you don't have to expend the fuel to get to the Moon - you only have to get within 150,000km of it (the Moon is ~400,000km from the Earth), and then the Moon's gravity will draw you in. The cost of getting to the Moon is much lower than getting to Mars, and you gain all these advantages. NASA's Artemis program places a small space station named Gateway in orbit around the moon, from which tasks such as provisioning and refuelling might take place. In addition, Gateway supports lunar surface operations. Bonus!

Both hydrogen and nitrogen can be extracted from the lunar regolith, and hydrogen and oxygen can be extracted from water. The Moon is now thought to potentially have large deposits of water available in the form of ice in craters at the poles which offer permanent shadow. There may be water-ice below the regolith in other places too. This means it may well be possible to manufacture hydrazine (H₂N₄) and perhaps other fuels, reducing the need to get them off the Earth and across to the Moon.

As a staging post for Mars missions, Gateway is an important step forward.

The current plans for Gateway would have it in a near-rectilinear halo orbit taking it over both poles (roughly 7 to 7.76 days per orbit). At the furthest distance from the Moon, it would be at a lunar altitude of 70,000km. The escape velocity from that point would require a ΔV of around 0.36km/s, meaning much more of the energy spent by the engines goes towards getting on the Hohmann transfer ellipse (or hyperbolic arc if on a fast transfer) than breaking free of orbit. The ΔV for getting to and from the lunar surface is measured in metres per second, not kilometres.

A more in-depth article about Gateway can be found on Wikipedia's Lunar Gateway page.

The starting point of any mission is deciding it's profile.

• What are the objectives of the mission?
• Does the mission have to get there as quickly as possible?
• Does the mission have to return?
• Is limiting the amount of total travel time a priority?

Consider the above questions with and without a crew, and with and without robotic landers. Some landers (possibly rovers) may want to return material to Earth. What the mission intends to do once it gets to Mars usually dictates what method is used to get there (and return if required).

Purely robotic missions, whether that's putting a lander/rover on the surface or a satellite into orbit, will usually take the easiest and cheapest route: a Hohmann transfer orbit. Crewed missions will generally want to get there faster, but they'll also want a high degree of safety - which an untested hyperbolic fast-transfer won't give them, so if that's the intention, testing and perfecting the technology (and verifying the maths) for such a transfer needs to begin decades ahead of time.

New and more powerful engines open up new possibilities for making the journey in different ways. Specialised software is calculating trajectories that super-computers struggled with just a couple of decades ago.

These are not all the options, and I'm sure more will come in the future.

• Twitter
• Facebook
• Google+
• LinkedIn
• Pinterest
• Tumblr
• Reddit
• Taringa
• StumbleUpon
• Telegram
• Hacker News
• Xing
• Vk
• Email